 En cirkel har ligning
`(x-4)^2+(y-3)^2=5^2`
En cirkel har ligning
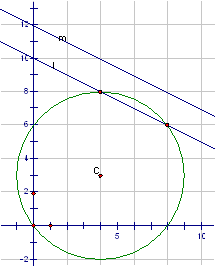
`(x-4)^2+(y-3)^2=5^2`og en linje, l, har ligning `y=-1/2x+10`
Vi vil bestemme skæringspunkter mellem cirklen og linjen
 En cirkel har ligning
`(x-4)^2+(y-3)^2=5^2`
En cirkel har ligning
`(x-4)^2+(y-3)^2=5^2`
og en linje, l, har ligning `y=-1/2x+10`
Vi vil bestemme skæringspunkter mellem cirklen og linjen
Skæringspunkter koordinater skal passe i begge ligninger. Vi har altså to
ligninger med to ubekendte: x og y. Vi kan nu slippe af med y ved at erstatte y
med den tilsvarende x-formel fra l:
`(x-4)^2+(-1/2x+10-3)^2=5^2`
som er en andengradsligning.
For at løse skal vi gange parenteser ud og ordne efter faldende potenser af
x:
`x^2-8x+16+1/4x^2-7x+49=25`
`5/4x^2-15x+40=0`
Andengradsligningen har diskriminant
`d=(-15)^2-4*5/4*40=25`
og løsninger
`x=(15+-sqrt(25))/(2*5/4)`
`x=8` og `x=4`
Til de fundne x-værdier kan vi beregne y-værdier ved at indsætte i linjens
ligning
`x=8` : `y=-1/2*8+10=6` som giver
skæringspunktet (8,6)
`x=4` : `y=-1/2*4+10=8` som giver
skæringspunktet (4,8)
Vi kan gennemføre tilsvarende beregninger med linjen m: `y=-1/2x+12`
Her vil beregningerne stoppe, når vi når til diskriminanten, som bliver negativ.
Konklusionen bliver her, at der ikke er nogen skæringspunkter mellem cirklen og
linjen m.
Hvis vi kun vil vide, om linjen skærer cirklen, ikke hvor
linjen skærer cirklen, kan vi nøjes med at beregne afstanden fra cirklens
centrum til linjen.
Hvis denne afstand er mindre en cirklens radius, vil linjen skære cirklen to
steder.
Hvis denne afstand er større en cirklens radius, vil linjen ikke skære cirklen.
Hvis denne afstand er lig med radius, vil linjen tangere cirklen.
Se nærmere om cirkeltangenter på en følgende side.
`dist(l,C)=|3-(-1/2*4+10)|/sqrt(1+(-1/2)^2)=5/sqrt(5/4)<5`
Altså skærer linjen, l, cirklen to steder, som vi allerede har set ovenfor.
`dist(m,C)=|3-(-1/2*4+12)|/sqrt(1+(-1/2)^2)=7/sqrt(5/4)=6.3>5`
Altså skærer linjen, m, ikke cirklen
Hvis alternativt en af, eller begge de givne linjers ligninger er på form `a*x+b*y+c=0` , kan du først isolere y, og så anvende fremgangsmåden ovenfor.