Arealet af en cirkel

Vi skal se, hvordan man kan nå frem til en formel for arealet af en cirkel ud fra kendte arealer af polygoner, som tilnærmer cirklen.

Første tilnærmelse er et indskrevet kvadrat, P4. Kvadratets areal er ikke nogen god tilnærmelse til cirklens areal, men det er enkelt at beregne. Centervinklen i en trekant fra cirklens centrum ud til to af firkantens nabopunkter er en ret vinkel. Trekanten har derfor areal    `T=1/2*r*r`  hvor r er cirklens radius. Firkanten består af 4 sådanne trekanter og har derfor et samlet areal på    `P_4=2r^2` Anden tilnærmelse er en regulær indskrevet ottekant, P8. Centervinklen er på  `360/8=45` grader, og en lille centertrekant har areal    `T_8=1/2*r*r*sin(45)` og hele ottekanten består af 8 centertrekanter og den har derfor samlet areal på    `P_8=4*r^2*sin(45)`

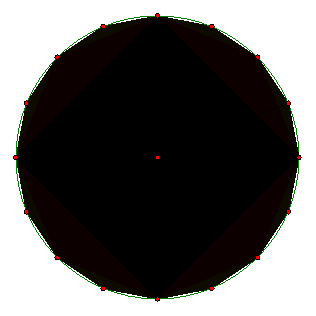Tredie tilnærmelse er en regulær indskrevet 16-kant, P16. Centervinklen er på  `360/16=22.5` grader, og en lille centertrekant har areal    `T_16=1/2*r*r*sin(22.5)` Hele 16-kanten består af 16 centertrekanter og har derfor samlet areal på    `P_16=8*r^2*sin(22.5)` Generelt får har en regulær n-kant en lille centertrekant med areal  `T=1/2*r^2*sin(360/n)` Den regulære polygon består af n sådanne trekanter og har derfor samlet areal    `P_n=n*1/2*r^2*sin(360/n)`

Ved tilnærmet beregning (4 decimaler) af formlen ovenfor med r=1 fås

n	4	8	16	32	64	128	256
Pn	2	2.8284	3.0615	3.1214	3.1365	3.1403	3.1413

og vi ser, at n-kant arealerne vokser op mod et tal på godt og vel 3.

Med et mellemvægts-matematikprogram som for eksempel TI InterActive kan vi lave symbolsk grænseovergang og får
    `lim_(n->oo)(n/2*r^2*sin(360/n))=pi*r^2`
Hermed har vi "bevist", at cirkelarealet som grænseværdi for n-kantsarealerne er lig med `pi*r^2`

Oldtidens grækere beregnede polygonarealer som tilnærmelser til tallet `pi`.
De gjorde sig tanker i stil med ovenstående, selv om de hverken havde sinusfunktionen eller grænseværdibegrebet til rådighed (for slet ikke at tale om matematikprogrammer til symbolske beregninger).

Det er muligt, men ikke simpelt inden for B-niveauets rammer, at lave grænseovergangen i "beviset" ovenfor med håndkraft. Herefter er argumentet et "rigtigt" bevis.

Fremgangsmåden ovenfor kan benyttes til en lang række af andre beregninger, for eksempel tangenthældning.
Det skal vi se nærmere på i afsnittet om differentialkvotient.

Idéen er her, at vi tilnærmer tangentens hældning med hældningen for en sekant gennem to grafpunkter.
En sekant er normalt ikke det samme som en tangent, men hvis de to grafpunkter vælges meget tæt, vil sekantens hældning ligge tæt ved tangentens hældning.

Tangentens hældning fremkommer nu som grænseværdi for alle sekanthældninger, hvor sekantens ene grafpunkt går imod sekantens andet grafpunkt.