Med TI83/84
Med formler
Bestemmelse af konstanterne i en harmonisk svingning
y=a∙sin(b∙x+c)+d
med TI83/84 ud fra kendt graf
![[image]](images/TIIimagefile10289.gif) TI83/84 kan tilpasse en harmonisk svingning,
TI83/84 kan tilpasse en harmonisk svingning,
y=a∙sin(b∙x+c)+d
dvs
bestemme konstanterne a, b, c og d, ud fra mindst 4 kendte punkter.
Metoden kaldes sinus-regression, sinreg, som betyder, at maskinen finder den
svingning, som passer bedst muligt (ligger tættest ved) en række givne
punkter (mindst 4).
Hvis der kræves at svingningen skal beskrives med
y=a∙cos(b∙x+c)+d
kan du først finde "sinuskonstanterne" som nedenfor, og så til slut
oversætte sin til cos med formlen
sin(x)=cos(
π
2
−x
)=cos(
x−
π
2
)
Først skal TI83 have en liste af kendte x-værdier:
{1,2,3,4,5} STO L1
hvor L1 ligger over 1-tasten
Så skal TI83 have en liste af kendte y-værdier:
{2,5,2,-1,2} STO L2
hvor L2 ligger over 2-tasten.
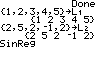 Så skal sinreg startes
med
Så skal sinreg startes
med
STAT CALC SinReg
Afslut med ENTER
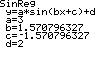 Nu viser TI83 de
beregnede konstanter.
Nu viser TI83 de
beregnede konstanter.
Den færdige formel med korrekte konstanter sat ind ligger i systemvariablen
RegEQ, hvorfra den kan plottes.
 Først skal den ind i
Y-editoren:
Først skal den ind i
Y-editoren:
Y= RegEQ
hvor RegEQ hentes ved at taste VARS Statistics
EQ RegEQ ENTER
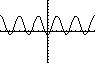 Nu kan grafen vises
med GRAPH
Nu kan grafen vises
med GRAPH
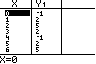 Og svingningen kan
også tjekkes med TABLE
Og svingningen kan
også tjekkes med TABLE
Vi ser, at tabellen passer med de oprindelige punkter.
Med TI83/84
Med formler
Bestemmelse af konstanterne i en harmonisk svingning
ud fra kendt bund og top
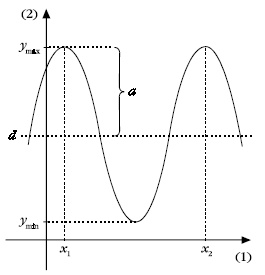 Om en svingning
Om en svingning
f(x) = a∙sin(b∙x + c) + d eller
g(x) = a∙cos(b∙x + c) + d
gælder, at den
- svinger med ±a om niveauet d,
så Vm(f) = [d-a;d+a]
, når a>0
- og har perioden
T=
x
2
−
x
1
=
2π
b
Konstanterne a og b kan bestemmes ud fra aflæsning af ymax og
ymin ved at løse ligningerne:
d + a = ymax og d - a = ymin
hvoraf fås
d=
y
max
+
y
min
2 og
a=
y
max
−
y
min
2
Konstanten b kan bestemmes ved at løse ligningen
2π
b
=
x
2
−
x
1
hvoraf fås
2π
x
2
−
x
1
=b
Konstanten c kan endelig findes ved at sætte mange kendte
størrelser ind i svingningsformlen.
I tilfældet sinus får vi
ymax = a∙sin(b∙x2+c) + d
hvor kun c er ubekendt.
Vi kan så isolere c og får
c=
sin
−1
(
y
max
−d
a
)−b⋅
x
2
I tilfældet
cosinus får vi
ymax = a∙cos(b∙x2+c) + d
hvor vi igen kan isolere c og får
c=
cos
−1
(
y
max
−d
a
)−b⋅
x
2
![[image]](images/TIIimagefile10289.gif) TI83/84 kan tilpasse en harmonisk svingning,
TI83/84 kan tilpasse en harmonisk svingning,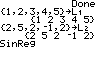 Så skal sinreg startes
med
Så skal sinreg startes
med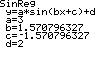 Nu viser TI83 de
beregnede konstanter.
Nu viser TI83 de
beregnede konstanter. Først skal den ind i
Y-editoren:
Først skal den ind i
Y-editoren: Nu kan grafen vises
med GRAPH
Nu kan grafen vises
med GRAPH Og svingningen kan
også tjekkes med TABLE
Og svingningen kan
også tjekkes med TABLE Om en svingning
Om en svingning