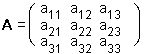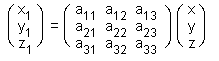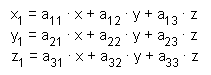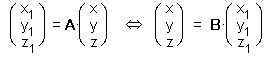Drejning i rummet

Kubens akse kan vippes efter x, y og z aksen.

Hvis kuben skifter drejningsretning, skyldes det et synsbedrag, idet du bytter om på kubens inder- og yderside. Denne ombytning kan også forekomme, selvom kuben ikke bevæger sig.

Matematikken gennemgås nedenunder.

Hvis vi drejer om en af koordinatakserne, kan vi umiddelbart overføre resultaterne fra plangeometrien. Hvis vi fx. drejer om z-aksen, må z-koordinaten jo være konstant, og drejningen kan derfor angives således:

x' = xcos(v) - ysin(v)

y' = xsin(v) + ycos(v)

z' = z

Hvis vi drejer om en vilkårlig valgt akse, indfører vi et ekstra koordinatsystem med den givne akse som z-akse, og foretager drejningen i det koordinatsystem. Så kan vi jo umiddelbart bruge formlen ovenfor, men det kræver selvfølgelig, at vi for det første skal konstruere koordinatsystemet, og for det andet, at vi skal transformere koordinaterne til det nye system. Og når vi har drejet punkterne, skal vi transformere dem tilbage igen, så de kan afsættes i det oprindelige koordinatsystem.

Vi kan let konstruere basisvektorerne i det nye koordinatsystem ved at finde tre indbyrdes ortogonale enhedsvektorer:

vælg først en vektor vinkelret på aksens retningsvektor, og beregn dernæst vektorproduktet af de to vektorer, og normaliser tilsidst alle tre vektorer.

Det er langt værre at transformere koordinaterne. Det kræver i virkeligheden kendskab til Lineær algebra (matrixregning). Vi vil her nøjes med at beskrive teorien :

En 3x3 matrix er et skema med 3 rækker og 3 søjler : Det første index er rækkeindexet og det andet er søjleindekset. Matricer betegnes normalt med store (fede) bogstaver.
Enhver koordinattransformation i rummet mellem sædvanlige retvinklede koordinatsystemer med samme Origo, er bestemt ved hjælp af en matrix
Højresiden udregnes (ganges) ved at danne skalarprodukterne af rækkerne med (x,y,z)
Det er altid muligt at finde en entydig bestemt løsning (x, y, z) til ligningssystemet, dvs. at finde den omvendte transformation. Matricen B kaldes den inverse matrix til A, og omvendt. Vi skriver A = B^-1 og B = A^-1

Vi vender nu tilbage til vores problem, hvor vi kender B, idet dens søjler består af koordinaterne (i det gamle system) til basisvektorerne i det nye koordinatsystem. Derfor kender vi transformationen fra det nye til det gamle system, men vi skal også bruge A, som er den inverse til B. Det er ret kompliceret at beregne den inverse matrix (se nedenfor), men de fleste graflommeregnere kan gøre det uden videre.

Den endelige metode bliver dermed: (hvis det nye koordinatsystem har begyndelsespunkt i (a,b,c))

Træk (a,b,c) fra koordinaterne til punktet
Transformer koordinaterne, dvs. gang A med koordinatsættet
Drej om z-aksen i det nye koordinatsystem
Transformer tilbage igen, dvs. gang B med det fremkomne koordinatsæt og læg dernæst (a,b,c) til igen.

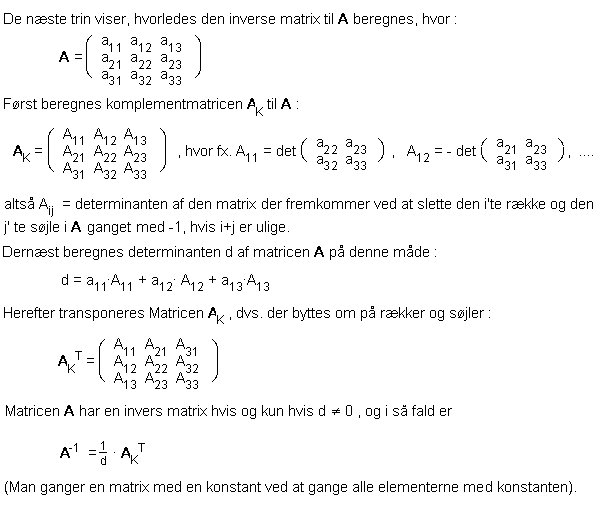
Den omvendte matrix kan også bestemmes ved at løse 3 ligninger med 3 ubekendte, se Gauss-elimination.

Drejning (plangeometri) - Planer i rummet

02/2004/pmh