Gør rede for de grundlæggende regninger med komplekse tal.
Gør rede for, hvordan komplekse tal kan fremstilles som vektorer i den komplekse talplan, og for, hvordan de grundlæggende regninger ser ud her. Begrund de Moivres formel.
Giv eksempler på metoder til løsning af ligninger.
De metoder, du omtaler, skal du belyse ved at bruge dem til løsning af opgaver. Du kan bruge opgaverne nedenfor. De fleste af disse opgaver skal behandles.
1. Et komplekst tal z er givet ved z=(1+2i)2+13i/(2-3i). Skriv z på formen x+yi.
2. Bestem de komplekse tal z, for hvilke z2+Re z+Im z =0.
3. Bevis, at der for vilkårlige komplekse tal z og w, hvor w¹ 0, gælder, at
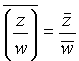
4. To komplekse tal z og w er givet ved
![]()
Bestem modulus og argument for hvert af tallene z, w, z+w, z·w, 1/z og z3.
5. Om et komplekst tal z oplyses, at |z| = 2,58 og arg z = 218,5°. Skriv z på formen x + yi.
6. Løs ligningen z3=4+3i
7. Løs ligningen z2=5-12i
8. Løs ligningen z2+iz+1=0.
Jens Carstensen. Komplekse tal. 2. udgave 1987.