Lidt om statistisk testteori.

 

Allerførst: Statistisk testteori i det statistiske verdensbillede. Passende forsimplet.

 

Klassisk inferensteori: Sandsynligheder er frekvenser, eller logiske sandsynligheder.

 

Modsætningen hertil er Bayesiansk Statistik, hvor sandsynlighedsbegrebet tolkes bredere- en sandsynlighed må her godt være subjektiv! Man kan således godt tale om sandsynligheden for regn i dag.

 

Begge ”skoler” anerkender, at sandsynligheder skal opfylde de grundlæggende aksiomer for at man kan regne på og med dem

 

S= udfaldsrum ={a,b,c,d,…..}

A, B, C, ..=hændelser = delmængder af S

P= sandsynlighedsmål på S

P(Ø)=0

P(S)=1

P(A U B)=P(A)+P(B), for A∩B=Ø

 

Neyman-Pearson testteori, med oprindelse i 1930’erne hører tættest til den klassiske inferensskole. Men heller ikke her, er alle lige store fans!

Testteori har sin helt store berettigelse i fx kvalitetskontrol- og enhver mediciner med respekt for sig selv kender grundbegreberne fra det testteoretiske univers.

 

Testteori kræver, at man deler sit verdensbillede op i (to) hypoteser:

 

En nulhypotese, H0, og en alternativ hypotese, H1.

 

De to hypoteser er asymmetriske i den forstand, at H0 er den hypotese, vi vil tro på, indtil den er ”modbevist”.

 

Det statistiske test udføres ved beregning af en teststørrelse -  test statistic, som man kan forudsige opførslen af, forudsat at H0 er den sande tilstand af verden.

 

 

Eksempel:

 

Kast med mønt:

Jeg påstår, min mønt er ”ægte” - altså, der er lige stor sandsynlighed for at få plat som krone.

I holder på plat - jeg på krone. Taberen afleverer en 10’er for hver gang den andens side kommer op.

 

Vi kaster 10 gange.

1.     Det bliver 10 gange krone

2.     Det bliver 9 gange krone

3.     Det bliver 8 gange krone

4.     Det bliver 7 gange krone

5.     Det bliver 6 gange krone

6.     Det bliver 5 gange krone

7.     Det bliver 4 gange krone

8.     Det bliver 3 gange krone

9.     Det bliver 2 gange krone

10.                   Det bliver 1 gange krone

11.                   Det bliver 0 gange krone

 

Hvilke af disse udfald vil gøre, at I holder op på at tro på, at jeg taler sandt om den ”ægte” mønt?

 

De interessante er de ekstreme udfald - altså ekstreme i forhold til H0,!

 

Formelt set:

Modellen siger, at antallet af krone ud af 10 kast er bin(10,p), hvor p=P(krone i et kast), altså et mål for møntens ægthed.

H0: p=1/2

H1: p>1/2          

 

Formulering af hypoteserne på denne måde kræver, at man har en vis portion tillid til mine åndsevner – husk hypoteserne skal tilsammen dække alle muligheder!

 

Antag, at udfaldet blev 8 krone. Det vil være nemt at udregne, hvor stor sandsynligheden for dette udfald er, HVIS H0 er sand.

 

Sandsynlighedsfunktionen for binomialfordelingen, n=10, p=1/2

 

x               P(X=x)

0               0.001  

1               0.010 

2               0.044 

3               0.117 

4               0.205 

5               0.246 

6               0.205 

7               0.117 

8               0.044 

9               0.010

10             0.001   

 

Dvs, hvis mønten er ægte er P(antal krone =8) =0.044.

Vi kunne tage denne sandsynlighed som testsandsynlighed - men for at have samme fundament for både diskrete som kontinuerte stokastiske variable bruger vi i stedet

P(antallet af krone mindst lige så ekstremt som det sete) = P(X≥8)=0.055.

Denne størrelse kaldes testsandsynligheden- eller p-værdien.

 

Det vi har lavet her, kaldes et parametrisk test. Det er desuden et eksakt test. Og så er det ensidet.

 

Nu er det op til os at afgøre, om denne p-værdi er så lille, at vi vil holde op med at tro på H0.

 

Til tider er der udefra kommende krav til, hvornår man skal forkaste sin H0. Det kan fx være når p≤0.05. Nogle bestemte faste grænser som 1%, 5% eller 10% har ligesom fastlagt sig pr tradition i nogle sammenhænge. De faste grænser er tæt forbundne med det, der kaldes et signifikansniveau, der ofte er lig med den faste grænse for forkastelse.

 

Hvis vi arbejder med en fast grænse på 5% for forkastelse, så kan vi se af tabellen ovenover, at vi vil forkaste hypotesen om den ægte mønt, hvis vi ud af 10 kast får 9 eller 10 gange krone. Vi kan altså oversætte vores test direkte til et kritisk område i udfaldsrummet. I dette tilfælde vil sandsynligheden for at få en observation i det kritiske område, hvis mønten er ægte – altså under H0, være P(X=9)+P(X=10)=0.011.

 

Sandsynligheden for at få en observation i det kritiske område, under H0, altså her α=0.011, kaldes signifikansniveauet for testet.

Signifikansniveauet for et test angiver sandsynligheden for at forkaste en sand nulhypotese - en type 1 fejl.

 

Som oftest vil man kunne få sin faste grænse til at passe med sit signifikansniveau- at det ikke kan lade sig gøre her skyldes, at vi har en diskret stokastisk variabel- og et eksakt test.

 

Tilbage til eksemplet.

Vi fastholder strategien med at forkaste hypotesen om møntens ægthed, hvis vi får 9 eller 10 krone ud af 10 kast. Vi har set, at det giver en sandsynlighed på 0.011 for, på forkert grundlag, at anklage mig for uærlighed.

 

Den anden fejl vi kan begå – fejl af type 2 – at acceptere en falsk nulhypotese, kan også kvantificeres.

 

Hvis min mønt faktisk ER lidt skæv – altså H1 er den rigtige hypotese, og P(krone i et kast) = 0.8, så vil sandsynligheden for at I faktisk opdager det, med den fastlagte strategi være 0.268+0.107=0.375. Sandsynligheden for IKKE at opdage det, vil så være 1-0.375=0.625.

 

Styrken af et test er givet ved sandsynligheden for at for forkaste H0 som funktion af den sande parameter. Sandsynligheden for at lave en type 2 fejl er 1-styrken.

 

 

Styrkefunktionen bruges til at lave strategier for stikprøvekontroller.

 

Der udtages stikprøver af leveret vareparti for at sikre at det lever op til kvalitetskravene.

 

Nulhypotesen er, at partiet er i orden.

Signifikansniveauet angiver leverandørrisikoen

Sandsynligheden for at lave en type 2 fejl ved en bestemt overskridelse af kravene er modtagerrisikoen.

Man kan så regne ud, hvor stor stikprøven skal være, for at leve op til de aftalte krav.

 

 

Et par andre simple test:

 

Vi vil lave et test for om en maskine, der putter sukker i poser til 1 kg er indstillet rigtigt. Hvis den er indstillet rigtigt, skal middelværdien af posernes vægt være 1 kg. Der er en tilfældig variation i afvejningerne svarende til en standardafvigelse på 20 g.

 

X=stokastisk variabel=vægt af sukkerposen

 

Model: X ~ N(μ,σ2), hvor σ2=0.0202.

 

H0: μ=1

H1 : μ≠1

Vi tager en stikprøve på 10 poser og kontrolvejer dem.

Det viser sig, at de har en gennemsnitsvægt på 0.990 kg.

 

Vi skal nu afgøre, om maskinen skal justeres.

 

Teststørrelse( =Z=U)=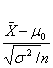 ==-1.58

 

Teststørrelsen er N(0,1) fordelt under H0 !

 

Testet er tosidet – hvilket vi ser i H1 . Både store og små værdier er kritiske for nulhypotesen.

 

 

 

 

 

P-værdien er 2*P(Z≥1.58)=2* 0.057= 0.114

DVS. det er ikke klart påvist, at maskinen skal justeres.

 

Hvis vi ikke havde kendt variansen, skulle vi i stedet have haft den estimeret ud fra data ved 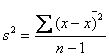. Og vi skulle have brugt en anden teststørrelse:

Teststørrelse =t=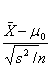

 

Teststørrelsen er Student-t fordelt med (n-1)frihedsgrader under H0 – FORUDSAT antagelsen om normalitet holder.

 

Som sidste test tager vi endnu et test for andel:

 

Vi vil teste, om der er flere mænd end kvinder, der handler i Harald Nyborg. Så vi stiller op og registrerer, hvor mange mænd og hvor mange kvinder, der er blandt 200 kunder.

Antallet af mænd =X, p=P(en kunde er en mand), n=200.

X~bin(200,p)

 

H0: p=1/2

H1 : p≠1/2

 

Vi registrerer, at der er 122 mænd ud af de 200 kunder.

Hvis vi ville lave testet eksakt skulle vi bare gøre som i eksemplet med mønten- dvs summe over sandsynligheden for alle udfald, der er mere ekstreme end det observerede. Det gider vi ikke! Vi laver et approximativt test.

Teststørrelse =Z=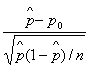

Hvis  kan man bruge normalfordelingen  og .   

 

Teststørrelsen udregner vi til 3.1894, hvilket er ekstremt i normalfordeling. Det ville det også være, hvis vi havde testet ensidet.